아래는 프로그래머스 lv2 문제 거리두기 확인하기 링크이다.
↓ ↓ ↓
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
문제
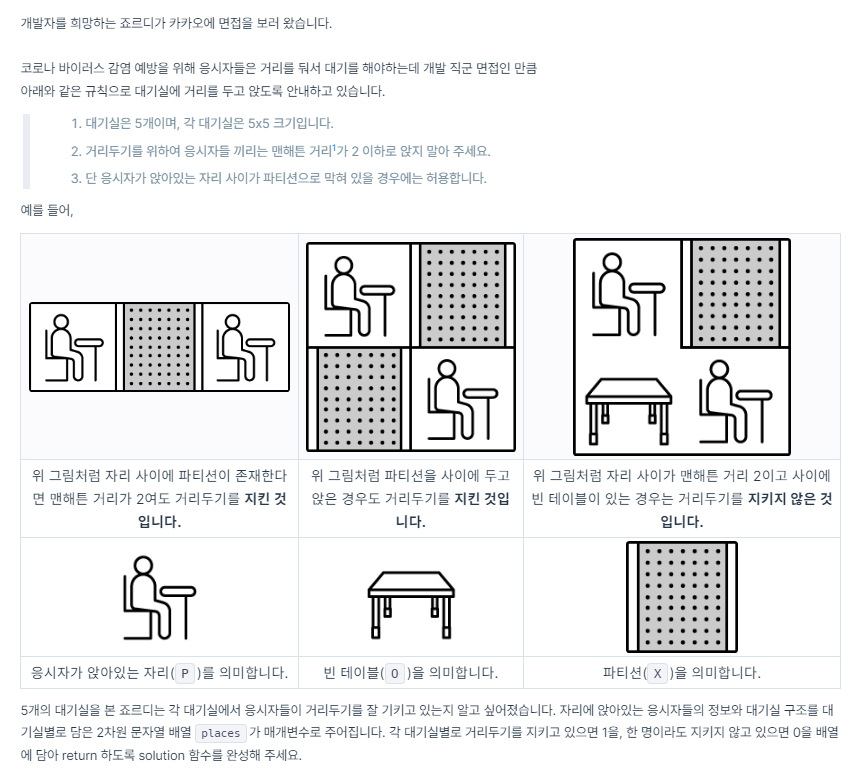

문제가 level2이지만 맨해튼 거리는 뭐고 뭔가 거창해(?) 보여서 살짝 쫄렸다.
한번 쭉 읽고 두 번째 예제를 보니 이해가 빨리 됐다.
역시 프로그래머스는 예제 설명이 친절하다.
[문제 정리]
- 제한 사항을 보면 주어진 그래프는 5x5 고정이다.
- P의 상하좌우에 P가 있으면 거리두기 실패
- P의 상하좌우에 O가 있을 때 그 O의 상하좌우에 P가 있으면 거리두기 실패 (자기 자신 제외)
- X는 상관없음
이렇게 가정하고 바로 코드를 작성했는데 결과는 통과했지만 깔끔한 느낌이 없어서 아쉬웠다.
문제 정리 세 번째에서 P의 상하좌우에 O가 있으면 bfs(nx, ny) 함수를 재귀를 돌고 싶었지만 전역변수를 지정해야 하는 기분 탓에 한번 시도해 보고 안돼서 접었다. 나름 시간복잡도 생각에 최대한 전역변수는 쓰고 싶지 않았다..
(혹시 재귀로 풀으신 분이 있다면 한 수 알려주세요!!)
풀이
아래 코드는 이차원 리스트를 하나씩 탐색하다가 P가 나오면 거리두기를 지켰는지 확인을 했다.
거리두기 확인은 P의 상하좌우에 P가 있으면 바로 0을 리턴해줬고,
P의 상하좌우에 O가 있으면 그 O의 상하좌우에 P가 2개 이상인지 확인을 했다.
(처음 자기 자신 P는 무조건 상하좌우 어디든 속해있기 때문에 2 이상을 카운트함)
try except 문을 사용한 이유는 현재 그래프에서 거리두기가 지켜지지 않았을 때,
바로 다음 그래프로 넘어가고 싶어서 사용했다.
다중 반복문을 빠져나오기 위함이다.
코드
class LoopBreak(Exception):
pass
def bfs(x, y, graph):
dx = [0,1,0,-1]
dy = [-1,0,1,0]
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if nx < 0 or ny < 0 or nx > 4 or ny > 4:
continue
if graph[nx][ny] == 'P': # P 상하좌우에 P가 있으면 바로 0 리턴
return 0
elif graph[nx][ny] == 'O': # O가 있으면 상하좌우에 P가 2개 이상인지 확인
cnt = 0
for j in range(4):
nx2 = nx + dx[j]
ny2 = ny + dy[j]
if nx2 < 0 or ny2 < 0 or nx2 > 4 or ny2 > 4:
continue
if graph[nx2][ny2] == 'P':
cnt += 1
if cnt > 1:
return 0
else:
return 1
def solution(places):
answer = []
for place in places:
try:
# 이차원 리스트 생성
graph = []
for p in place:
graph.append(list(p))
# P가 있을때 거리두기 지켰는지 확인
for x in range(5):
for y in range(5):
if graph[x][y] == 'P':
res = bfs(x,y,graph)
if res == 0:
answer.append(0)
raise LoopBreak() # 바로 다음 그래프로 이동
answer.append(1)
except LoopBreak:
pass
return answer
5x5 배열로 크기가 크지 않아서 경우의 수를 전부 고려한 분도 있고, 사람마다 풀이 방법이 다양했다.
'코딩테스트 준비 > 문제풀이' 카테고리의 다른 글
| [프로그래머스/Python] PCCP 기출문제 1번 붕대감기 - 코딩테스트 (0) | 2025.02.26 |
|---|---|
| [프로그래머스/Python] PCCP 기출문제 3번 충돌위험 찾기 풀이 (0) | 2025.02.24 |
| [프로그래머스/파이썬] PCCP 기출문제 2번 퍼즐 게임 챌린지 - 이분탐색 (0) | 2025.02.23 |
| [프로그래머스/Python] PCCP 기출문제 1번 동영상 재생기 - 파이썬 (0) | 2025.02.22 |
| [백준] 11404번 플로이드 워셜 알고리즘 설명 - 파이썬 with python (0) | 2025.02.20 |
