[Algorithm] 최단 거리 알고리즘 종류 총정리(다익스트라, 플로이드, 벨만포드) with Python

다익스트라, 벨만포드, 플로이드 워셜은 모두 최단 거리를 구할 때 사용하는 알고리즘입니다.

사실 공부한거 나중에 까먹으면 한눈에 보고 싶을 것 같아서 포스팅으로 정리한 건데

잘못된 부분이 있다면 댓글로 따끔하게 일침 부탁드립니다. 감사합니다.

 

---

▶ 다익스트라 알고리즘

 

(백준 1753번 최단경로 문제에서 나온 예제입니다.)

 

다익스트라 알고리즘은 엣지값이 양수일때만 사용이 가능하고 시작점에서 다른 모든 노드까지의 최단 거리를 구합니다.

최단 거리 리스트는 1차원 리스트로 출발 노드는 0, 나머지는 무한대로 초기화해주고,

그래프는 인접 리스트 [[] for _ range(n)] 형태로 생겼습니다.

visited = [False] * (n+1)		# 방문 여부 리스트
graph = [[] for _ in range(n+1)]	# 그래프
dist = [float('inf')] * (n+1)		# 최단 거리 리스트
dist[start] = 0

 

힙큐(우선순위 큐)를 사용해서 방문하지 않은 노드 중 가장 최단거리 노드부터 탐색하도록 합니다.

D[1]+2와 D[2]를 비교하면 min(0+2, inf) 이므로 D[2]는 더 작은 값인 2로 업데이트되며

D[1]+3과 D[3]을 비교하면 D[3]=3으로 업데이트됩니다.

 

방문리스트를 만들어서 방문했던 곳은 다시 안 가도록 처리하고 모든 노드가 선택될 때까지 반복합니다.

while heap:
    dist, node = heapq.heappop(heap)
    if visited[node]:
       continue
    visited[node] = True
    for nextnode, nextdist in graph[node]:
        if dist[nextnode] > dist[node] + nextdist:
            dist[nextnode] = dist[node] + nextdist
            # 가중치가 정렬 기준이므로 (가중치, 도착노드) 순으로
            heapq.heappush(heap, (dist[nextnode], nextnode))

 

다익스트라 알고리즘의 기본 문제로 백준 1753번 최단경로를 추천드리며,

아래 링크는 다익스트라 알고리즘 해설과 코드이므로 참고하시길 바랍니다.

 

[백준] 1753번 최단경로 / 파이썬 python 다익스트라 알고리즘 구현

 

---

▶ 벨만 포드 알고리즘

 

(백준 11657번 타임머신 문제에서 나온 예제입니다.)

▷ 최단거리 리스트 D[N]을 n-1번 실행하는 과정 알아야할 점! 벨만 포드는 한번 수행할때마다 출발노드가 무한대가 아닌 모든 엣지를 전부 훑는다. (1번째 과정) 출발 노드가 무한대면 안되므로 초기값에서 1번만 먼저 봄. 1 → 2 에서 D[2] 와 D[1]+4 를 비교 후 작은 값인 4를 D[2]에 넣어줌 : 0 4 0 1 → 3 에서 D[3] 과 D[1]+3 을 비교 후 작은 값인 3을 D[3]에 넣어줌 : 0 4 3 이제 2와 3이 무한대가 아니므로 2번도 훑어봄. 2 → 3 에서 D[3] 과 D[2]-4 를 비교 후 작은 값인 0을 D[3]에 넣어줌 : 0 4 0 3 → 1 에서 D[1] 과 D[3]-2 를 비교 후 작은 값인 -2를 D[1]에 넣어줌 : -2 4 0 (2번째 과정) 모든 출발 노드가 무한대가 아니므로 전부 훑는다. 1 → 2 에서 D[2] 와 D[1]+4 를 비교 후 작은 값인 4를 D[2]에 넣어줌 : -2 2 0 1 → 3 에서 D[3] 과 D[1]+3 을 비교 후 작은 값인 3을 D[3]에 넣어줌 : -2 2 0 2 → 3 에서 D[3] 과 D[2]-4 를 비교 후 작은 값인 0을 D[3]에 넣어줌 : -2 2 -2 3 → 1 에서 D[1] 과 D[3]-2 를 비교 후 작은 값인 -2를 D[1]에 넣어줌 : -4 2 -2

 

벨만 포드 알고리즘은 다익스트라와 비슷하지만 가중치가 음수인 경우도 수행이 가능합니다.

음수 사이클의 유무 판단으로 많이 사용되는데, 음수 사이클이 존재하면 최단 거리를 구할 수 없습니다.

 

다익스트라와 벨만포드 모두 단일 시작점 최단 경로 알고리즘으로

한 시작점에서 다른 모든 정점까지의 거리를 구해줍니다.

 

최단 거리 리스트는 1차원 리스트로 출발 노드는 0, 나머지는 무한대로 초기화해주고,

그래프는 엣지 중심인 엣지 리스트로 만듭니다.

dist = [float('inf')] * (n+1)		# 최단 거리 리스트
dist[1] = 0

graph = []				# 엣지 데이터 저장
for _ in range(m):
    s, e, v = map(int, input().split())
    graph.append([s,e,v])

 

엣지의 최대 개수는 노드가 n개일 때 n-1개입니다.

출발노드는 무한대이면 안되고 D[e] > D[s] + v 일 때 D[e] 값은 D[s] + v 로 업데이트 해줍니다.

for _ in range(n-1):
    for start, end, value in graph:
        if dist[start] != float('inf') and dist[end] > dist[start] + value:
            dist[end] = dist[start] + value

 

n-1번 수행했을 때와 n번째 수행했을 때 값이 달라졌다면 음수사이클이 존재한다는 의미이므로

마지막에 한번 더 업데이트를 시도해 봅니다.

n-1인 2번 수행했을 때 결과와 n=3번째 결과가 다르므로 음수 사이클이 존재합니다.

고로 최단 거리를 구할 수 없다는 결론이 나옵니다.

 

벨만 포드 알고리즘의 기본 문제로 백준 11657번 타임머신을 추천드리며,

아래 링크는 벨만 포드 알고리즘 해설과 코드이므로 참고하시길 바랍니다.

 

[백준] 11657번 타임머신 | 벨만 포드 알고리즘 파이썬 Python

 

---

▶ 플로이드 워셜 알고리즘

 

(백준 11404번 플로이드 문제에서 나온 예제입니다.)

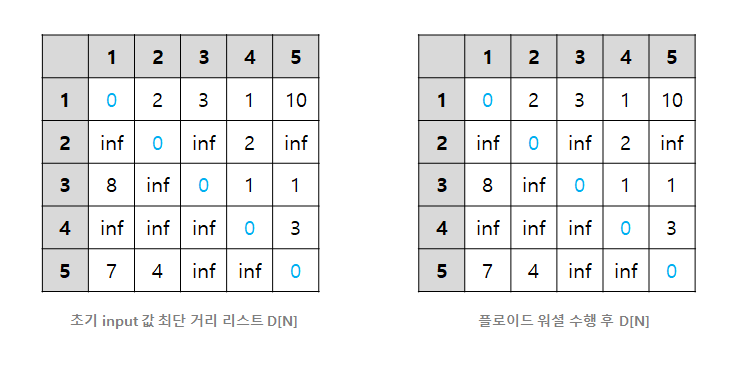
▶ 최단거리 리스트 D[N]을 실행하는 과정 D[start][end] 보다 D[start][k] + D[k][end]가 작으면 업데이트 (k: 경유지)

 

플로이드 워셜 알고리즘은 모든 정점 쌍의 최단 거리를 구하기 때문에 2차원 리스트로 생겼고

시간복잡도가 O(𝑉^3) 이므로 다익스트라와 벨만 포드보다 시간 복잡도가 좋지 않습니다.

따라서 노드 수가 몇백 개 이하로 적을 때 사용합니다.

 

플로이드 알고리즘도 벨만포드와 마찬가지로 가중치가 음수인 경우도 수행이 가능합니다.

핵심 이론은 start에서 end까지 최단 경로를 구했을 때

최단 경로 위에 경유지 k가 있다면 start → k, k → end 경로 역시 최단 경로라는 것입니다. 

 

최단 거리 리스트 D[N]의 2차원 리스트 초기값은 출발점과 도착점이 같은 (k, k) 자리는 0으로,

나머지는 무한대 inf로 초기화해줍니다.

 

플로이드 워셜 알고리즘을 수행해서 결과값을 도출하면 되는데

플로이드 워셜 로직은 외워두는 게 좋습니다.

 

바깥쪽 반복문부터 차례대로 경유지, 출발지, 도착지 순서로 돌리며

플로이드 워셜의 점화식은 D[start][end] = min(D[start][end], D[start][k] + D[k][end]) 입니다.

# 경유지, 출발지, 도착지 순으로
for k in range(n):
    for start in range(n):
        for end in range(n):
            if D[start][end] > D[start][k] + D[k][end]:
                D[start][end] = D[start][k] + D[k][end]

 

플로이드 알고리즘의 기본 문제로 백준 11404번을 추천드리며,

아래 링크는 플로이드 워셜 알고리즘 해설과 코드이므로 참고하시길 바랍니다.

 

[백준] 11404번 플로이드 워셜 알고리즘 설명 - 파이썬 with python