https://www.acmicpc.net/problem/1753
백준 1753번 최단경로 문제는 다익스트라 알고리즘을 사용했다.
참고로 다익스트라 알고리즘은 출발 노드에서 모든 노드 간의 최단 거리를 구하며 엣지는 양수이어야 한다.
문제

설명
다음은 1753번 문제에 대한 풀이 순서이다.
1) 최단 거리 리스트 D[N]은 1차원 리스트로 출발 노드는 0, 그 외는 모두 무한대로 초기화한다.
2) D[N]에서 현재 값이 가장 작은 노드를 골라서 연결된 다른 노드의 값을 없데이트 한다.
최단 거리 업데이트는 min(현재 노드 최단 거리 값 + 가중치, 다음 노드 최단 거리 값) 으로 비교한다.
3) 방문 리스트 visited[]를 만들어서 재방문 하지 않고 모든 노드가 선택될 때까지 반복한다.
글만 보면 헷갈릴 수 있으니 그림을 보고 설명해보겠다.
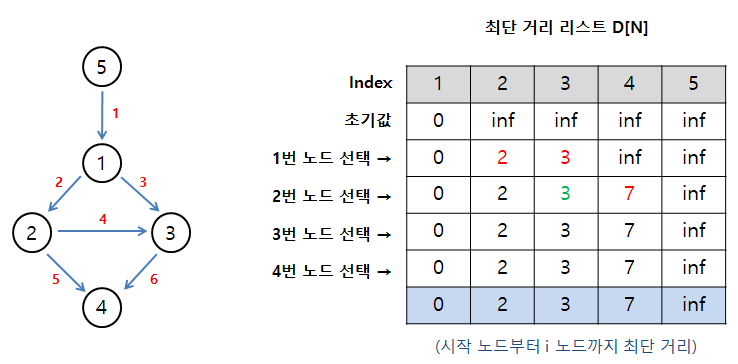
처음에 1번 노드를 선택했을때 노드 2와 3을 힙큐(heapq)에 저장한다.
여기서 힙큐를 쓰는 이유는 방문하지 않은 노드 중 가장 최단거리 노드를 선택하기 위함이다.
(코드를 보면 알겠지만 가중치가 정렬 기준이며, 우선순위 큐를 써도 된다.)
D[1]+2 와 D[2] 를 비교하면 min(0+2, inf) 이므로 D[2]는 더 작은 값인 2로 업데이트 되며,
D[1]+3 과 D[3] 을 비교하면 D[3] = 3으로 업데이트 된다.
그리고 최단 거리 리스트 D[N]에서 값이 가장 작은 2번 노드를 선택하면 3과 7 노드가 힙큐에 저장되며
노드 3에서 D[2]+4 와 D[3]을 비교하면 min(2+4, 3) 이므로 기존에 있는 값이 신규 값보다 작기 때문에
업데이트를 하지 않는다.
이렇게 모든 노드를 방문할 때까지 진행하면 시작 노드부터 i 노드까지 최단 거리 리스트가 완성된다.
코드
import heapq
import sys
input = sys.stdin.readline
V, E = map(int, input().split())
start = int(input())
dist = [float('inf')] * (V+1) # 거리 저장 리스트
visited = [False] * (V+1) # 방문 여부 체크리스트
graph = [[] for _ in range(V+1)]
for _ in range(E):
u, v, w = map(int, input().split())
graph[u].append((v, w))
heap = []
heapq.heappush(heap, (0,start))
dist[start] = 0
while heap:
nowDist, nowNode = heapq.heappop(heap)
if visited[nowNode]:
continue
visited[nowNode] = True
for nextNode, nextDist in graph[nowNode]:
if dist[nextNode] > dist[nowNode] + nextDist:
dist[nextNode] = dist[nowNode] + nextDist
# 가중치가 정렬 기준이므로 (가중치, 도착노드) 순서
heapq.heappush(heap, (dist[nextNode], nextNode))
for i in range(1, V+1):
if visited[i]:
print(dist[i])
else:
print("INF")'코딩테스트 준비 > 문제풀이' 카테고리의 다른 글
| [백준] 1850번 최대공약수 파이썬 Python / 유클리드 호제법 풀이 (0) | 2025.02.14 |
|---|---|
| [백준] 1012번 유기농 배추 | 파이썬 Python 너비 우선 탐색(BFS)으로 구현 (0) | 2025.02.11 |
| [백준] 1931번 회의실 배정 | 파이썬 Python 그리디 알고리즘 구현 (0) | 2025.02.10 |
| [백준] 2178번 미로 탐색 / 파이썬 python 너비 우선 탐색(bfs) 구현 (0) | 2025.02.10 |
| [백준] 1717번 집합의 표현 / 파이썬 Python (union find) (0) | 2025.02.09 |
